8. Physical process options¶
8.1. Equation of state approximation¶
Todo
put in link for state_nml Equation of state namelist
Four options for computing the density from salinity and potential temperature are available. The first is an equation of state introduced by McDougall, Wright, Jackett and Feistel (MWJF [16]) which is a faster and more accurate alternative to the UNESCO equation of state. The second is a UNESCO equation of state based on potential temperature from Jackett and McDougall (JMCD [12]). The third is a polynomial fit to the full UNESCO equation of state. The advantage of the polynomial form is that it is faster; the disadvantage is that the polynomial is only valid over a specified temperature and salinity range and exceeding that range will have unpredictable results. This is a particular issue with the KPP vertical mixing scheme which often computes buoyancy by displacing water near the surface to deep water where the EOS range has been restricted. The last option is a linear eos which is supplied for use only in special situations where such an approximation is appropriate.
r the polynomial option, there are two methods for determining the
polynomial coefficients and these are determined by the value of
state_file. If this variable is defined as ‘internal’, the code
will determine the polynomial coefficients internally based on the
vertical grid. The internal routines currently use hard-wired profiles
for the limits of validity of the polynomial eos; if the user wishes
to change these limits, they can be changed in an off-line coefficient
generator (in the tools/eos directory) and the coefficients can be
read in from a file. The value of state_file will be the name of
the coefficient input file. As mentioned above, the polynomial eos has
a certain temperature and salinity range over which the polynomial is
valid. The state_range_opt variable determines what to do if these
limits are exceeded during a simulation. The first option is to simply
‘ignore’ when these occur; this is generally not as bad as it sounds
as the range is valid for nearly all normal cases. The second option
is to ‘check’ whether the range is exceeded and print a warning if
such problems are detected. The last option, ‘enforce’, simply makes
sure the polynomial is evaluated within the correct range without
changing the values of T or S. For example, if the temperature drops
below -2C, the code will compute a density based on a temperature of
-2C without actually changing the temperature. The
state_range_freq can be used to perform the checks infrequently to
save computational time.
8.2. Baroclinic-mode parameters¶
Todo
put in link for baroclinic_nml Baroclininc namelist
The reset_to_freezing option exists to make sure the surface
temperature does not drop below freezing, a situation that can occur
with some types of forcing in stand-alone mode. This option should be
disabled if sea ice formation is enabled (see the next section).
8.3. Sea-ice emulation parameters¶
Todo
put in link for ice_nml Sea-ice emulation
If ice_freq_opt is not ‘never’, the code will create ice whenever
the ocean temperature drops below freezing at levels higher then
kmxice. This ice formation will be computed at frequencies
determined by the ice_freq in ice_freq_opt units.
ice_freq_opt should always be set to ‘coupled’ to compute ice formation on coupling timesteps.
The resulting heat and water fluxes associated with ice formation are saved
and sent to the flux coupler for use in the ice model.
8.4. Topographic stress¶
Todo
put in lnk for topostress_nml Topographic stress namelist
If ltopostress is .true., then an implementation of a topographic
stress parameterization is enabled. In effect, this changes the
field acted on by the Laplacian operator from 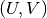 to
to 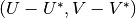 where
where 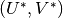 are derived based on the topography gradient and a
specified length scale (note that this only works for Laplacian
mixing). A smoothed topography can be used to compute this gradient with
the number of smoothing passes with a 9-point averaging stencil is
governed by
are derived based on the topography gradient and a
specified length scale (note that this only works for Laplacian
mixing). A smoothed topography can be used to compute this gradient with
the number of smoothing passes with a 9-point averaging stencil is
governed by nsmooth_topo.