Getting started#
Hello, and welcome to MusicBox! Here, we will be covering some basic usages of the MusicBox library.
What is MusicBox?#
MusicBox is a library with a Python API for box modeling that builds on top of MUSICA, a collection of modeling software that allows for robust modeling of chemistry in Earth’s atmosphere. Boxes refer to a set of adjacent grid cells that represent the exchange of information.
1. Downloading MusicBox#
To install MusicBox onto your device, run
$ pip install acom_music_box
Note: Installing MusicBox will automatically install MUSICA, a required dependency of MusicBox that is used throughout this tutorial.
2. Importing MusicBox#
To import your newly-downloaded MusicBox into a Python file, as well as some other libraries so that this demo can run:
from acom_music_box import MusicBox, Conditions
import musica.mechanism_configuration as mc
import matplotlib.pyplot as plt
3. Defining a System#
In MusicBox, a system is defined by a mechanism that includes:
a set of species and their respective phases, and
a set of reactions that the species participate in.
The system is the fundamental building block of MusicBox and is your main concern when using this library. The following steps will walk you through:
creating your own system,
solving your system, and
viewing and visualizing your results.
3a. Defining Species#
A species is simply a reactant or product in a chemical reaction. You have the freedom to name a species anything in MusicBox, just make sure that it is logical to you. For extended documentation about the Species class, go here. Here is a snippet that defines three chemical species:
# Create each of the species that will be simulated
X = mc.Species(name="X")
Y = mc.Species(name="Y")
Z = mc.Species(name="Z")
species = {"X": X, "Y": Y, "Z": Z}
gas = mc.Phase(name="gas", species=list(species.values()))
This code block creates 3 species called X, Y, and Z and adds them to a dictionary called species. The variable name and the name of the species are not required to be the same, but it is strongly recommended so that your code is more organized. Next, a phase is created named “gas”. In MusicBox, phases are essentially collections of species that are assumed to be well-mixed. Note: Creating the species dictionary and the phase is mandatory, as subsequent code relies on the data being bundled in specific object types.
3b. Defining Reactions#
A chemical reaction is a process in which a set of reactants transforms into a set of products. To define a reaction in MusicBox:
# Create the reactions that the species undergo in the
arr1 = mc.Arrhenius(name="X->Y", A=4.0e-3, C=50, reactants=[species["X"]], products=[species["Y"]], gas_phase=gas)
arr2 = mc.Arrhenius(name="Y->Z", A=4.0e-3, C=50, reactants=[species["Y"]], products=[species["Z"]], gas_phase=gas)
rxns = {"X->Y": arr1, "Y->Z": arr2}
This code block uses the gas and species variables from the previous code block. Using the species and gas variables, it creates two reactions: arr1 and arr2. The arr1 variable represents the conversion of X (reactant) into Y (product) and defines Arrhenius rate constant parameters A and C. The arr2 variable is just like arr1, but instead it represents the conversion of Y (reactant) into Z (product). These reactions are then bundled into a dictionary called rxns just like the species before. More information on the Arrhenius reaction can be found here. Note: MusicBox allows for users to experiment with an array of reaction types. Go here to view a list of supported reactions and their parameters.
3c. Defining Mechanisms#
A mechanism represents a set of species with their respective phases and reactions. For extended documentation about the Mechanism class, go here. To create a mechanism in MusicBox:
# Create the mechanism that is defined by the species, phases, and reactions
mechanism = mc.Mechanism(name="tutorial_mechanism", species=list(species.values()), phases=[gas], reactions=list(rxns.values()))
This code block builds upon the previous two functions, using the previously-created species, phases, and reactions as arguments. It simply creates a mechanism variable that represents an instance of the Mechanism class. The mechanism is first given a name, then the species, phase, and reactions are passed into their respective arguments.
4. Creating a Box Model#
Box models allow you to solve your previously-created mechanism under conditions that can change the reactions’ rates over time. Each instance of the MusicBox class acts as an independent box model. You can also define the length of the simulations and the time steps. To initialize a new box model:
# Create the box model that contains the mechanism
box_model = MusicBox()
box_model.load_mechanism(mechanism)
This code block is straightforward, simply creating an instance of the MusicBox class and then loading the mechanism as an argument for the box model.
4a. Adding Initial Conditions to Your Box Model#
The initial conditions of the model define the environment the mechanism takes place in at the start of the simulation. Some conditions that are recommended to define for your system include:
the temperature, measured in Kelvin (K),
the pressure, measured in Pascals (Pa), and
the concentration of each of the species, measured in mol/m<sup>3</sup>.
For extended documentation about the Conditions class, go here. To set the initial conditions of your box model:
# Set the conditions of the box model at time = 0 s
box_model.initial_conditions = Conditions(
temperature=298.15, # Units: Kelvin (K)
pressure=101325.0, # Units: Pascals (Pa)
species_concentrations={ # Units: mol/m^3
"X": 3.75,
"Y": 5.0,
"Z": 2.5,
}
)
This code block sets the box model’s initial_conditons attribute. In the condition class, you should provide a temperature, pressure, air density (unless you just want it based on the Ideal Gas Law, which is the default), and each of the species’ concentrations as arguments.
4b. Adding Evolving Conditions to Your Box Model#
An evolving condition will change the environment of the mechanism at the defined time value. These changes can include species concentration, temperature, pressure, et cetera. To create an evolving condition for your box model:
# Set the box model conditions at the defined time
box_model.add_evolving_condition(
100.0, # Units: Seconds (s)
Conditions(
temperature=310.0, # Units: Kelvin (K)
pressure=100100.0 # Units: Pascals (Pa)
)
)
This code block is similar to the previous one for setting the initial conditions. Just like in the previous code block, a Conditions object is created as an argument for the box model’s add_evolving_condition() function. However, there is now a new value put at the very beginning of the function that represents the time at which the evolving conditions takes place at.
4c. Additional Box Model Configuration#
Box models contain some additional configuration options that need to be defined. These include:
the simulation length,
the chemistry step time, and
the output step time.
To set these configurations for your box model:
# Set the additional configuration options for the box model
box_model.box_model_options.simulation_length = 200 # Units: Seconds (s)
box_model.box_model_options.chem_step_time = 1 # Units: Seconds (s)
box_model.box_model_options.output_step_time = 20 # Units: Seconds (s)
This code block sets some of the attributes of the box model’s options, including:
simulation_length: the number of time steps that the simulation lasts for,
chem_step_time: the number of time steps between each simulation calculation, and
output_step_time: the number of time steps between each output of the model.
All three of these have seconds as their unit.
5. Running and Solving Your Box Model#
Now, you are able to run and solve your newly-created box model. To solve your box model, simply call its solve() function:
df = box_model.solve()
6. View Outputs and Visualizations#
MusicBox supports viewing your simulation’s outputs as well as visualizing them. To view your solved model and a basic visualization of it:
display(df)
df.plot(x='time.s', y=['CONC.X.mol m-3', 'CONC.Y.mol m-3', 'CONC.Z.mol m-3'], title='Concentration over time', ylabel='Concentration (mol m-3)', xlabel='Time (s)')
plt.show()
time.s |
ENV.temperature.K |
ENV.pressure.Pa |
ENV.air number density.mol m-3 |
CONC.X.mol m-3 |
CONC.Y.mol m-3 |
CONC.Z.mol m-3 |
|
|---|---|---|---|---|---|---|---|
0 |
0 |
298.15 |
101325 |
40.874 |
3.75 |
5 |
2.5 |
1 |
20 |
298.15 |
101325 |
40.874 |
3.41149 |
4.8714 |
2.96711 |
2 |
40 |
298.15 |
101325 |
40.874 |
3.10354 |
4.72528 |
3.42118 |
3 |
60 |
298.15 |
101325 |
40.874 |
2.82338 |
4.56584 |
3.86077 |
4 |
80 |
298.15 |
101325 |
40.874 |
2.56852 |
4.39669 |
4.28479 |
5 |
100 |
298.15 |
101325 |
40.874 |
2.33666 |
4.22086 |
4.69247 |
6 |
120 |
310 |
100100 |
38.8363 |
2.12702 |
4.04212 |
5.08087 |
7 |
140 |
310 |
100100 |
38.8363 |
1.93618 |
3.86147 |
5.45235 |
8 |
160 |
310 |
100100 |
38.8363 |
1.76247 |
3.6807 |
5.80683 |
9 |
180 |
310 |
100100 |
38.8363 |
1.60434 |
3.50128 |
6.14438 |
10 |
200 |
310 |
100100 |
38.8363 |
1.4604 |
3.32443 |
6.46517 |
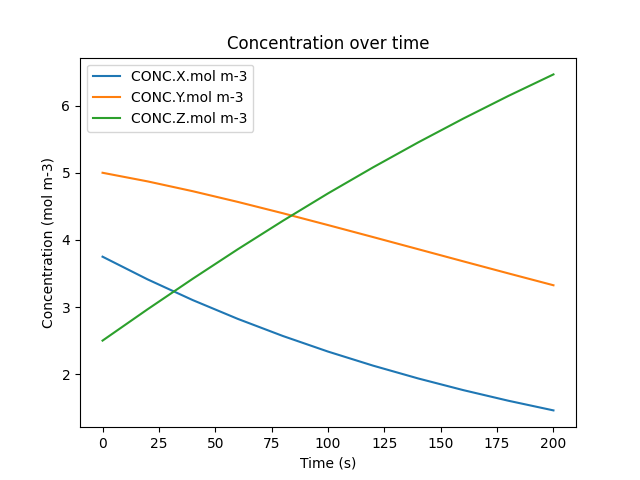
This code block prints out the output of the simulation that was just ran as well as it utilizing Python’s matplotlib library to visualize it. To do so, the plot() function is called, with the desired independent variable (time) and dependent variables (concentration of each species) being passed in. The plot is also given a title as well as a label for both the x-axis and the y-axis. Lastly, the show() function is called so that you can see the plot directly above this text.