Chapter 6: Place-Based Climate Projections

6.1 Introduction

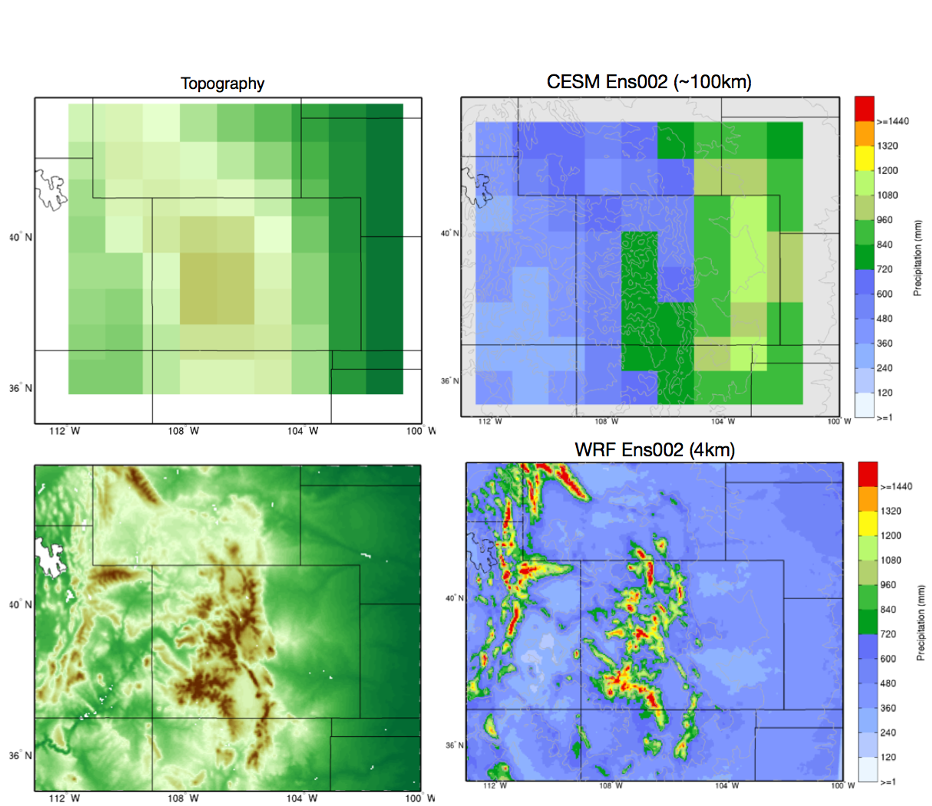
Despite continuing improvements in Global Climate Models (GCMs) and computational capabilities of high-performance computers, the spatial resolution of the current suite of GCMs is typically too coarse for use in project-specific applications. For example, the spatial resolution of the GCMs included in the most recent Coupled Model Intercomparison Project Phase 5 and 6 (CMIP5 and CMIP6) ranged from approximately 0.5 degree to 4 degrees in horizontal resolution or approximately 50 km to 400 km (Andrews et al. 2012; Taylor et al., 2012). To overcome resolution issues, downscaling is a common approach to translating climate change signals represented by climate models to changes in meteorological parameters at the regional and local scales (Gutmann et al. 2014; Kotamarthi et al. 2021). Downscaling bridges the gap between the coarse resolution of climate models and the finer scales needed for impact assessments that assess water resources, agriculture, ecosystems, and other sectors. An example of this discrepancy is highlighted in Figure 1, which compares simulated precipitation results from a coarse resolution GCM against a high resolution regional model, where it is evident that the high resolution model is capable of resolving important meteorological processes resulting in a much more realistic characterization of precipitation (source: Gutmann, personal communication, NSF NCAR).

Downscaling uses techniques aimed at enhancing the spatial and temporal resolution of data obtained from GCMs and is generally considered necessary in hydrologic analysis, which benefits from high-resolution climate data, with scales of a few kilometers at most and at daily or even hourly timescales (Bhuvandas et al. 2014; Vogel et al. 2023). Downscaling techniques are broadly categorized into two main types: statistical and dynamical, although there are many examples where techniques are blended together to improve the performance of regional climate information (Jang and Kavvas 2015; Le Roux et al. 2019; Vandal et al 2019; Hobeichi et al. 2023). Machine learning methods are also becoming more prevalent and promising as an efficient and cost effective approach to downscaling (Jebeile 2021; Hobeichi et al. 2023).

While each method has its pros and cons, it’s important to recognize that while these methods can enhance local scale details based on the coarser scale GCM data, they cannot influence the larger scale dynamics that actually occur in the climate system. However, new generations of climate models are addressing this issue, with some GCMs run at 5 k resolution globally, and a new generation of variable resolution models (Huang et al 2016; Rhoades et al. 2018) employing unstructured grids, which allows for high resolution in places of interest (e.g., the Sierra or Rocky Mountains) and lower resolution where detailed fields are not needed (i.e., the Oceans). These more recent methods are still being developed within the research community and their practical applications are limited to date. Given that it takes considerable effort to develop high-quality, useful climate datasets, practitioners have made use of datasets developed by the climate science community, with data distributions made available through accessible data portals.

Figure 1. Downscaling from coarse resolution grids of global earth systems models (top), with a horizontal grid spacing of about 100 km, to fine scales of a high resolution regional model at ~4 km grid spacing (bottom), Left panels show the representative topography and the resulting precipitation over the Rocky Mountains of Colorado (right panels). Note that the GCM precipitation (top right panel) is not just represented at coarser resolution, but there are significant biases in the GCM precipitation both spatially and in magnitude, different processes are simulated locally.

6.2 Approaches to downscaling

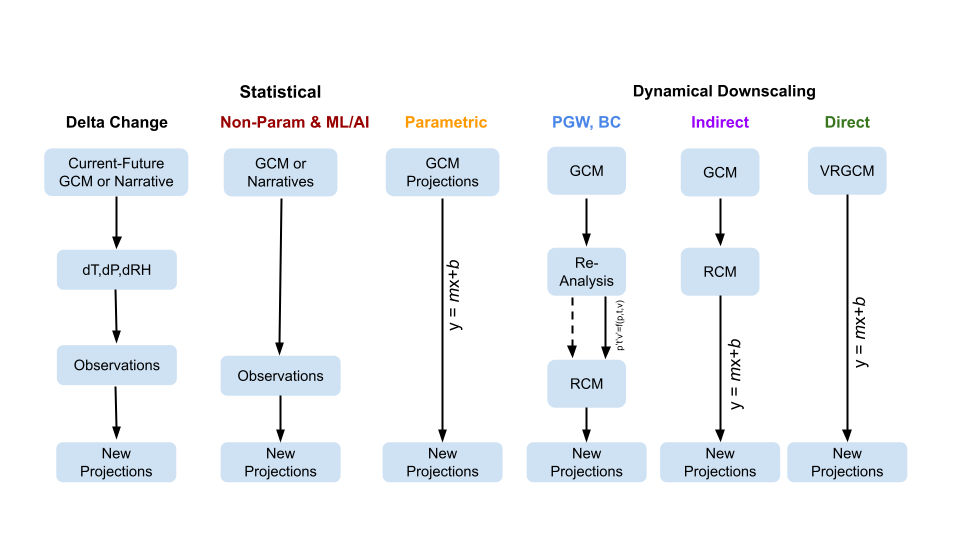
There are a multitude of techniques for translating coarse resolution GCM into fine-scale, local meteorological data useful for hydrologic modeling and analysis. Figure 5.1 provides a general summary of the approaches to downscaling, suggesting a ranking of methods from the ‘simpler’ approaches to the left and to the more complex and computationally intensive approaches to the right (Teutschbein and Seibert 2012; Vandal et al. 2019). While the figure suggests a given downscaling procedure will result in a usable dataset, the reality is that the various methods can include various combinations of approaches. The bottom line: There is some “art” to downscaling; there is no one single approach, and often the various methods are combined or blended based on the needs of the study.

From the figure, downscaling techniques include fairly simple “Delta Change” methods, to more sophisticated statistical methods that increasingly make use of machine learning, and dynamical methods, which use physical/process based models of the earth system (e.g., the atmosphere, ocean, land). Statistical downscaling uses statistical or mathematical relationships to refine coarse GCM output to a finer scale, while dynamical downscaling employs more physically based regional climate models to resolve finer-scale features. These regional models use the GCM output as boundary conditions to enhance resolution over smaller spatial domains.

Recent developments in machine learning have introduced new methods that blend some of the benefits and drawbacks of both statistical and dynamical approaches (Vandal et al. 2019). These techniques are applicable for enhancing both spatial and temporal resolution. In statistical methods, the modifications to spatial and temporal data can usually be handled separately, while dynamical downscaling allows for a flexible temporal resolution, because RCMs simulate the full 3-dimensional atmosphere that conserves mass, energy, and momentum and represents the energy and moisture budgets, with model time steps typically less than 1 minute. Statistical downscaling is typically not computationally expensive nor does it typically require large amounts of computing power or data storage, while dynamically downscaling typically requires High Performance Computing (HPC), which is both computationally and data intensive.

The Dynamical Downscaling approaches include the Pseudo Global Warming (PGW), which modifies historic meteorological data, such as the ERA5. PGW is similar to the statistical delta change approach, in that it maintains the same weather patterns; however, the dynamical model is able to resolve physical feedbacks in the climate system (e.g., convection). Even with dynamical downscaling, Bias Correction (BC) is often still applied after the generation of the meteorological dataset.

Figure 1. A summary of the various downscaling methods and their general characteristics, from the simpler Delta Change approach on the left, to non-parametric methods that rely on high-quality, long observational records; parametric methods that create statistical relationships between GCMs and surface variables (e.g daily precipitation and temperature), where the simple linear equation is used to imply the estimation of parameters (i.e. m,b); Pseudo Global Warming (PGW); Bias-Correction (BC), Variable Resolution Global Climate Model (VRGCM).

6.2.1 Statistical Downscaling

Statistical downscaling techniques can be employed to enhance both the temporal and spatial resolution of data, making it more applicable for hydrologic modeling applications. For hydrologic applications, the target variables are most often - daily Precipitation, Maximum and Minimum Temperature, sometimes Maximum and Minimum Relative Humidity, Windspeed, and Solar Radiation. Commonly, these are at a daily timestep, with some datasets available sub-daily.

There are various statistical methods available, each utilizing statistical relationships between broad-scale climate variables from General Circulation Models (GCMs) and observed local climate data to create finely tuned projections for specific areas. For instance, one might use high-resolution observed data and average it across the coarser grid squares of a GCM. On days when temperature and humidity in the observed, coarse data match those in the GCM data, it can be assumed that the high-resolution temperature and precipitation patterns for that day in the GCM will mirror those of the similar days in the observed data. Statistical downscaling methods include Delta Change (or change factor [morea about this below]) methods, regression techniques, weather generators, and weather classification strategies (Ekstrom et al., 2015). Each method has its own set of strengths and weaknesses, as detailed in Table 1. A generalized tool for evaluating and generating regional climate projections using a variety of statistical techniques has been developed by Gutmann et al. 2022, and available at https://github.com/NCAR/GARD.

Some advantages and disadvantages of statistical are as follows.

Statistical downscaling depends on the availability and quality of historical observational data for calibration. In regions with limited or poor-quality historical data, statistical downscaling might be limited. Generally, the statistical downscaling methods create relationships between historically observed climate and climate simulations from GCM output, with the assumption that the historical relationships will hold into the future. It is not clear that any statistical downscaling method can be relied on to represent changes in atmospheric phenomena that most GCMs do not simulate in the first place, such as major tropical cyclones and hurricanes.

Delta Change Methods

A simple, but informative method to explore climate change sensitivity of hydrologic systems is referred to as the “Delta Change” approach. It starts by exploring the observational record of climate variables like temperature, precipitation, wind speed, and others. This dataset represents the “baseline” or reference period. Then change factors are derived from global climate models, providing projections of how these climate variables might change in the future under various greenhouse gas concentration scenarios.

Delta-change factors are derived as the difference between the future climate projections of the GCMs against a historical baseline (usually averages over a specified reference period). For precipitation a ratio is typically used instead of a difference. These differences, or deltas, are typically expressed in terms of changes in mean temperature, precipitation amounts, etc., then applied to the historical data to build custom datasets. For example, if the delta for temperature is a +2°C increase, this change is added to the historical temperature records to generate a “future” dataset. A widely used method that employs the delta-change method has been promoted by the World Bank known as Decision Scaling (Brown et al. 2016). It uses a stress test approach to identify system vulnerabilities, and simple, direct techniques for the implementation of climate projections, such as the use of weather generators and delta-change that are informed by GCM results.

Non-Parametric Methods

In the context of downscaling global climate models (GCMs), “non-parametric” downscaling refers to statistical approaches that do not make assumptions about the underlying probability distributions of the variables involved. Instead, they use more flexible statistical techniques that can capture complex, nonlinear relationships between variables. Resampling techniques include bootstrap resampling or Monte Carlo resampling methods that can be used to generate ensemble datasets to represent uncertainty in the downscaling process without relying on specific parametric assumptions

Non-parametric downscaling methods offer advantages in capturing complex relationships and handling non-linearities in the climate system, which may be particularly important when downscaling GCM outputs to local or regional scales where these relationships can be highly variable. However, they may also require serially complete, spatially dense, and long-length datasets, and can be more computationally demanding than parametric methods.

Some of the more common Non-Parametric techniques include the following.

The Locally Constructed Analog (LOCA) method, constructs local analogs by identifying days in the historical observational record with similar large-scale climate patterns to those simulated by the climate model. The selected analogs are weighted based on their similarity to the target pattern and then interpolated to the desired observational grid.Focuses on single-variable analogs, with a primary emphasis on spatial patterns and high-resolution consistency with observations (Pierce et al. 2016).

The Multivariate Adaptive Constructed Analogs (MACA) downscaling method identifies analog days in the historical record that closely match the multivariate climate conditions of each day in the GCM simulations. These analogs are selected based on multiple climate variables (e.g., temperature, precipitation) to ensure a comprehensive representation of climate conditions. Once the analog days are identified, their observed weather patterns are used to construct a high-resolution climate dataset corresponding to the GCM projections. This involves combining the observed data from the analog days with the simulated data to generate downscaled outputs. MACA is considered “adaptive” as it allows for the ability to adjust the selection of analog days over time and space, ensuring that the downscaling remains relevant as climate conditions evolve. The primary difference between MACA and LOCA is that MACA uses a multivariate approach to downscaling, considering multiple climate variables simultaneously to construct analogs (Abatzoglou et al. 2012).

Machine-learning approaches such as support vector machines, random forests (He et al. 2016), neural networks, and kernel-based methods can be used to learn the relationship between large-scale and local-scale climate variables from historical data without assuming a specific functional form. A Machine Learning method by Benton et al. (2022) demonstrates how a neural network can be used to generate high spatial- and temporal-resolution wind and solar data from GCMs (Creswell et al. 2018). The approach uses generative adversarial networks or (GANs), which are trained on observed wind and solar data at 4-km hourly resolution against the same meteorological fields at 100-km resolution to learn the relationship between these variables across spatial scales. The model is then applied to downscale 100-km daily GCM output to 4 km hourly resolution, with the assumption that the relationships are the same in observational and GCM data, and will hold into the future (Buster et al 2024; Kochkov et al. 2024).

The Bias-Correction-Spatial Disaggregation (BCSD) is a well established method of statistical downscaling, whereby climate model outputs are corrected for systematic biases compared to observed data, which are then spatially interpolated to a finer grid. The bias correction usually entails quantifying the difference between the model output and observed data, often using quantile mapping, which matches the cumulative distribution functions (CDFs) of the model data with the observations. Spatial interpolation methods such as (eg. bilinear interpolation, nearest-neighbor interpolation) are then applied to the bias-corrected data at the GCM scale to a finer grid.

The K Nearest Neighbor algorithm, The k-Nearest Neighbor (k-NN) method is another statistical downscaling technique used to refine coarse-resolution climate model outputs to finer spatial resolutions. This approach relies on the similarity between observed and modeled data patterns to generate high-resolution climate projections. A unique aspect of K-NN is its ability to craft scenario “narratives” that are conditioned off of particular attributes of a GCM, such as drier and warmer, or “much drier and warmer” types of scenarios (Yates et al. 2005; Seyyed et al. 2012).

Parametric Methods

Parametric statistical downscaling employs statistical models that assume a specific functional form or distribution for the relationship between large-scale climate variables (predictors) and local-scale climate variables (predictands). These methods are called “parametric” because they involve fitting parameters of a predefined statistical model to the data. The parameters of the statistical model establish the relationship between large-scale climate variables (such as 500-millibar height, vertically integrated moisture, etc.) simulated by GCMs and local-scale climate variables at the downscale level (such as temperature and precipitation at specific locations). These parametric methods typically involve fitting regression models, such as linear regression or multiple linear regression, to historical climate data to establish the relationship between large-scale and local-scale variables.

A well established, statistical downscaling approach has been developed by Rob Wilby (Wilby 2004). Known as the Statistical DownScaling Model, SDSM is a climate scenario generation tool that uses a multiple linear regression technique to establish statistical relationships between large-scale predictors (such as those from GCMs) and local climate variables such as daily precipitation and temperature (predictands). The tool is available online, well documented in terms of understanding and implementation, and can be freely downloaded from the SDSM website (https://sdsm.org.uk/). SDSM has been used globally for various applications, including water-resource management, flood-risk assessment, and urban climate studies.

Table 1. A summary of statistical downscaling approaches, their pros and cons, and the availability of tools for their applications.

Downscaling Method	Pros	Cons	Tools/Data Available?
Delta Change	Simple to implement; insightful in terms of sensitivity	Not physically consistent. Unrealistic physical change.	Generally, method is simple enough to be directly used in a hydrologic model.
MACA- Multivariate Adaptive Constructed Analogs (MACA)	Considers multiple climate variables simultaneously,	Relies on quality of observational record. Needs a long obs record, more sophisticated due to multi-variate aspect. Assumes GCM spatial patterns contain necessary information.	A github R code is available, https://github.com/earthlab/cft
LOCA- Locally Constructed Analogs	Simpler in terms of handling single variables	Similar to MACA.	https://loca.ucsd.edu/
Bias-Correction Spatial Disaggregation (BCSD)	Maintains the statistical properties of historical observations (also a con); available globally and represent daily sequences	The spatially interpolated data can not represent spatial heterogeneity. Extremes are under-sampled, and wet-day frequency is poor.	https://ds.nccs.nasa.gov/thredds/catalog/AMES/NEX/GDDP-CMIP6/catalog.html
K-Nearest Neighbor (K-NN)	Simple and robust methods. Varying ways to implement to generate future climate projections	Relies on a high quality observational historical dataset (similar to MACA).	Both R and Python offer extensive KNN packages for generating downscaled data
En-GARD	Employs multi-variate relationships to predict each variable, may be more robust in the future.	Assumes historical relationships persist, may underpredict changes in extreme precipitation.	Code available on github https://www.github.com/NCAR/gard
AI and Machine Learning	Robust and efficient, powerful in finding relationships among variables. Computationally efficient	Assumes historical relationships will hold into the future. Can be difficult to implement, and somewhat of a black-box. Very new and not well characterized.	Both R and Python offer extensive machine learning packages that can be used for developing downscaling datasets
Pseudo-Global Warming	Generally easier to implement as a dynamical downscaling approach. Based on a historic period so can be more societally relevant	Can be physically inconsistent. Computationally expensive, large datasets that need post-processing, including bias-correction.
Parametric Statistical Downscaling-https://www.sdsm.org.uk/software.html	Statistically rigorous. Autocorrelation and cross-correlations between large-scale variables.	More effort to implement, need to develop statistical relationships. Selection of predictors should be explored	https://www.sdsm.org.uk/sdsmmain.html; https://climate-scenarios.canada.ca/?page=pred-cmip6

6.2.2 Dynamical Downscaling

Dynamical downscaling involves the combined use of both global and regional climate models (RCMs) to achieve higher spatial resolution and in some cases temporal resolution, over specific geographic areas. Traditionally, RCMs ingest outputs from GCMs as boundary conditions—assuming GCM data to be accurate at the edges of the RCM’s domain—and provide more detailed regional climate information. While RCMs can be applied to any location, their high-resolution design makes them computationally intensive, typically limiting their application to regions a few thousand kilometers on a side, given sufficient resources. RCMs offer enhanced flexibility in variable outputs and maintain more physically consistent results. However, RCM-downscaled outputs can retain biases from the GCM inputs and may introduce additional uncertainties. This reality means that RCM inputs are frequently bias corrected before running the RCM, and RCM outputs commonly require an additional post-processing step typically in the form of a bias correction. Nevertheless, RCMs can improve the representation of fine-scale weather variability influenced by local or micro-climate conditions, which are crucial for understanding extreme weather events that impact hydrologic systems.

The Weather Research Forecast Model (WRF)

The Weather Research Forecast Model (WRF) - The WRF model is one of the most widely used dynamical downscaling tools available for conducting Regional Climate Modeling experiments. The WRF model is a state of the art mesoscale numerical weather prediction system designed for both atmospheric research, operational forecasting applications, and more recently, regional climate-change projection development, where it is used to downscale ESM outputs to a finer resolution, typically on the order of a few kilometers, to study regional climate features. This process allows for more detailed simulations of local climate processes that GCMs might miss due to their coarser grid resolutions.

The WRF model serves a wide range of meteorological applications across scales from tens of meters to thousands of kilometers. The effort to develop WRF began in the latter 1990s and was a collaborative partnership of the National Center for Atmospheric Research (NCAR), the National Oceanic and Atmospheric Administration (represented by the National Centers for Environmental Prediction (NCEP) and the Earth System Research Laboratory), the U.S. Air Force, the Naval Research Laboratory, the University of Oklahoma, and the Federal Aviation Administration (FAA).

WRF can produce simulations based on actual atmospheric conditions (i.e., from observations and analyses), idealized conditions, and future climate projections driven by ESMs. WRF offers operational forecasting a flexible and computationally efficient platform, while reflecting recent advances in physics, numerics, and data assimilation contributed by developers from the expansive research community. WRF is currently in operational use at NCEP and other national meteorological centers as well as in real-time forecasting configurations at laboratories, universities, and companies. WRF has a large worldwide community of registered users (a cumulative total of over 57,800 in over 160 countries as of 2021), and NCAR provides regular workshops and tutorials on its use.

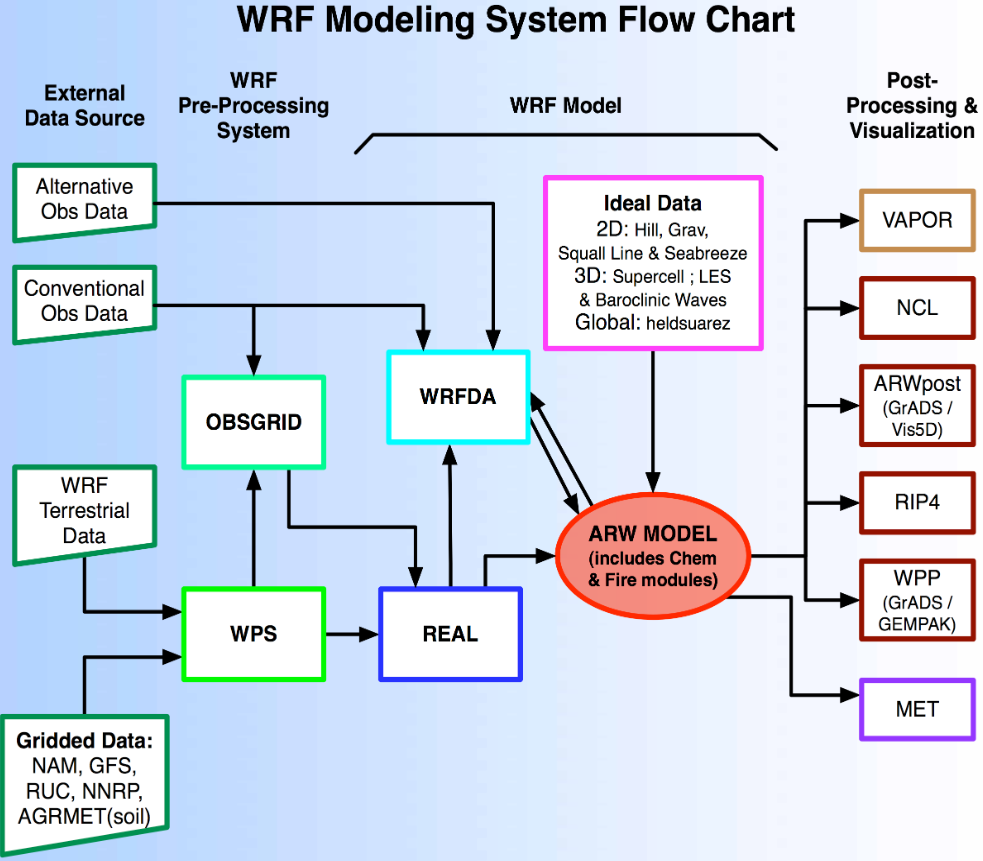
Figure: The Workflow for the WRF Model, used for both an operational implementation or a future regional dynamical downscaling experiment.

This site, https://www.mmm.ucar.edu/models/wrf, provides general background information on the WRF Model and its organization and offers links to information on user support, code contributions, and system administration. For detailed information on model use, updates and events, support, code downloads, and documentation, please visit the WRF-ARW github users page (https://github.com/wrf-model/Users_Guide).

Similar to statistical downscaling, many institutions provide publicly available dynamically downscaled products. However, these products often have limitations on the number of years, scenarios, regions, and variables they cover. The Coordinated Regional Climate Downscaling Experiment (CORDEX) produced such products, designed to evaluate regional climate-model performance through a series of experiments, including generating regional climate projections (Giorgi & Gutowski 2015). Over North America, the NA-CORDEX archive includes many dynamically downscaled projections (http://www.na-cordex.org). Although CORDEX data are readily accessible, its primary focus on model intercomparison means that other dynamically downscaled products might be better suited for specific regions and applications. In addition, CORDEX data have historically been relatively coarse in spatial resolution (>= 25 km) and have not included a bias correction of the global model data, and thus are not well suited for regional hydrologic applications, where spatial gradients and their influence on weather and climate are critical to represent.

Intermediate Complexity Models

Fully dynamical Global and Regional Climate models are expensive to run, because they require substantial computation for simulating both past and future climate. A novel alternative to the full physics models is what is known as the suite of intermediate complexity models. One such model is NSF NCAR’s Intermediate Complexity Atmospheric Research (ICAR) model which is a simplified atmospheric model designed primarily for climate downscaling and atmospheric sensitivity testing (Gutmann et al. 2016). ICAR is a quasi-dynamical downscaling approach that uses simplified wind dynamics to perform high-resolution meteorological simulations 100 to 1000 times faster than a traditional atmospheric model and can therefore be used to better characterize uncertainty across numerical weather prediction models and climate models, and in dynamical downscaling (https://github.com/NCAR/icar).

Pseudo Global Warming

The PGW approach involves modifying historical weather data with future climate-change signals derived from global climate models (GCMs) to simulate specific weather events to represent future climate conditions. This method allows researchers to isolate the influence of climate change on weather events by comparing the outcomes of the modified (pseudo-warmed) simulations against the original historical data with a shorter simulation time period. However, this method does not permit the model to project changes in the frequency of large-scale weather patterns such as atmospheric rivers or tropical cyclones. The PGW approach can be considered a type of “narrative, what-if, or storyline” approach, where the climate of the past is assumed to repeat in the future, but the meteorological fields are perturbed to reflect, for example, a “warmer and moister environment” (Rhoades et al. 2023). Some recently innovated tools that can be used to develop PGW datasets are available, such as those from Brogli et al. (2023).

An example of a PGW dataset, which has been developed as a collaboration between NCAR and USGS Water Mission Area is the CONUS404 (Rasmussen et al. 2023); a unique, high-resolution hydro-climate dataset appropriate for forcing hydrological models and conducting meteorological analysis over the conterminous United States. CONUS404, so named because it covers the CONterminous United States for over 40 years at 4-km resolution, was produced by the Weather Research and Forecasting (WRF) model simulations run by NCAR. The CONUS404 includes 42 years of data (water years 1980-2021) and the spatial domain extends into Canada and Mexico, thereby capturing transboundary river basins and covering all contributing areas for CONUS surface waters.

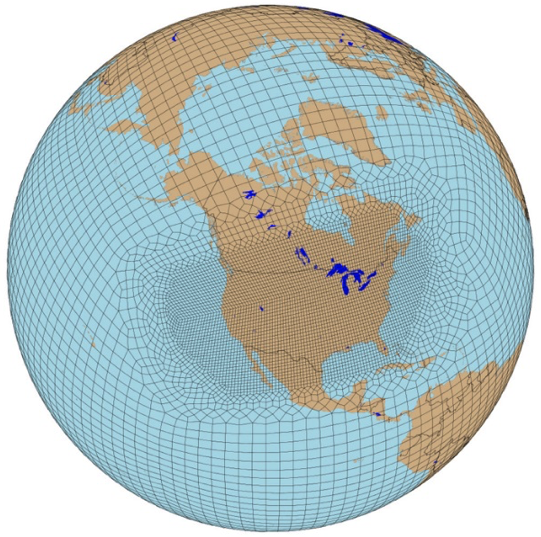
6.2.3 Variable Resolution GCMs

A new generation of global climate models takes advantage of a refined mesh that enhances the model’s ability to simulate climate processes with greater detail and accuracy in regions of interest while maintaining computational efficiency relative to running the entire globe at the higher resolution. This approach allows the model to focus computational resources on specific areas, such as coastlines, mountainous regions, or areas prone to extreme weather, without excessively increasing the overall computational cost.

An example of such a model is the U.S. Department of Energy’s, Energy Exascale Earth System Model ([E3SM] Zhang et al. 2024) model, a state-of-the-art Earth system model designed to run on exascale supercomputers. The E3SM model integrates components of the Earth system, including the atmosphere, ocean, sea ice, and land, to provide a comprehensive understanding of climate interactions and feedbacks.

6.2.4 Pre- and Post- Processing of Climate Models

Bias Correction

A reality of both GCMs and RCMs is that both are prone to biases due to our limited ability to represent the true state of the climate system because our representation of model physics, parameterizations and initial conditions are imperfect. These biases can significantly affect the accuracy and reliability of the downscaled climate projections. To address this, bias-correction techniques are often employed (Teutschbein and Seibert 2012; Mendez et al. 2020). Bias correction involves adjusting the model outputs to better match observed data. There are two primary stages at which bias correction can be applied: pre-bias correction and post-bias correction.

While dynamical downscaling with regional climate models (RCMs) helps refine the coarse resolution outputs of GCMs, both GCMs and RCMs are prone to biases due to imperfections in model physics, parameterizations, and initial conditions. These biases can significantly affect the accuracy and reliability of the downscaled climate projections. Additionally, if a hydrologic model is calibrated against an observed meteorological dataset, then the climate model outputs should contain similar statistical attributes, To address this, bias correction techniques are employed. Bias correction involves adjusting the model outputs to better match observed data. There are two primary stages at which bias correction can be applied: pre-bias correction and post-bias correction.

Pre-bias correction is applied before the dynamical downscaling process. This involves adjusting the outputs of the GCMs before they are used as boundary conditions for the RCMs. The advantage of pre-bias correction is that it ensures the inputs fed into the RCMs are already adjusted for biases, which can lead to more accurate boundary conditions and potentially more accurate downscaled outputs. This method helps align the large-scale drivers with observed data, which can be particularly beneficial in regions where the RCMs’ performance is highly sensitive to the accuracy of the boundary conditions. For example, many GCMs have too much moisture along the west coast of North America. This results in RCM simulations with snowpacks that are too deep, and as a result, the snow albedo feedback effect is not simulated correctly, and the degree to which it affects future air temperature changes is a function of the bias in the GCM rather than to the true physical processes (Kim et al. 2020). However, a modest bias correction to the boundary conditions dramatically improves this representation and decreases the spread of future projected changes in air temperature. In other regions, GCM biases have been shown to significantly inhibit the formation of tropical cyclones, as such the changes in tropical cyclones can not be simulated accurately without removing the large scale biases in wind shear and atmospheric stability (Akhter et al. 2023).

Post-bias correction is applied after the dynamical downscaling process. This method adjusts the outputs of the GCNs and RCMs to match observed data. The main advantage of post-bias correction is that it directly targets the biases in the high-resolution climate projections produced by the GCMs and RCMs (Chen et al. 2021). This approach allows for the correction of biases introduced at both the GCM and RCM stages. Post-bias correction can be more flexible and targeted, as it deals directly with the final outputs used for impact studies and decision-making. Many end-users of climate-change data will compare the observed climate to the modeled climate without removing biases. Such comparisons reveal the bias in the model instead of the changes of interest. Similarly, threshold-dependent metrics (e.g., the number of days with a heat index greater than 100°F) are extremely sensitive to small biases in the underlying dataset. Finally, if there is a need to run impact models, such as hydrologic modes which are often carefully calibrated to a given observational dataset, it is important to bias-correct the downscaled data to retain the underlying statistical properties to maintain consistency with the hydrologic model calibration. A common approach to bias correction is quantile mapping, which is a statistical technique used to correct biases in climate model output by aligning the statistical distribution of model-simulated variables with observed data. The approach involves the following steps.

Cumulative Distribution Functions (CDFs): The CDF of the climate model output is compared to the CDF of the observational data for a particular variable (e.g., temperature, precipitation) over a historical period.
Mapping: A mapping function is created that adjusts the model outputs so that their CDF matches the CDF of the observations. This mapping can be applied to model projections to correct biases in future climate scenarios.
Application: The correction is applied to future climate-model simulations by transforming the model outputs using the mapping function derived from the historical period.

This approach is particularly effective in addressing systematic biases in climate models, especially for extreme values, by ensuring that the corrected model outputs better represent the observed climate distribution.

In summary, both pre- and post-bias correction techniques are essential for improving the reliability of downscaled climate projections. Pre-bias correction ensures that the inputs to RCMs are more accurate, potentially enhancing the overall downscaling process. Post-bias correction directly addresses the biases in the final high-resolution outputs, ensuring that the downscaled projections are more aligned with observed data. The choice between pre- and post-bias correction, or a combination of both, depends on the specific requirements of the study and the characteristics of the region and models being used.

6.3 References

Abatzoglou, J. T., & Brown, T. J. (2012). A comparison of statistical downscaling methods suited for wildfire applications. International journal of climatology, 32(5), 772-780.

Bhuvandas, N., Timbadiya, P. V., Patel, P. L., & Porey, P. D. (2014). Review of downscaling methods in climate change and their role in hydrological studies. Int. J. Environ. Ecol. Geol. Mar. Eng, 8, 713-718.

Brogli, R., Heim, C., Mensch, J., Sørland, S. L., & Schär, C. (2023). The pseudo-global-warming (PGW) approach: methodology, software package PGW4ERA5 v1. 1, validation, and sensitivity analyses. Geoscientific Model Development, 16(3), 907-926.

Brown, C., Weatherly, J., Mearns, L., Steinschneider, S., Wi, S., Case, M., Hayden, T., Koster, A., Bukovsky, M. and McCrary, R., 2016. Decision-Scaling: A decision framework for DoD climate risk assessment and adaptation planning. Strategic Environmental Research and Development Program (SERDP).

Buster, G., Benton, B. N., Glaws, A., & King, R. N. (2024). High-resolution meteorology with climate change impacts from global climate model data using generative machine learning. Nature Energy, 1-13.

He, X., Chaney, N. W., Schleiss, M., & Sheffield, J. (2016). Spatial downscaling of precipitation using adaptable random forests. Water resources research, 52(10), 8217-8237.

Lorenz, Edward N. (March 1963). “Deterministic Nonperiodic Flow”. Journal of the Atmospheric Sciences. 20 (2): 130–141.

Pinto, James O., Andrew J. Monaghan, Luca Delle Monache, Emilie Vanvyve, and Daran L. Rife. “Regional assessment of sampling techniques for more efficient dynamical climate downscaling.” Journal of climate 27, no. 4 (2014): 1524-1538.

Kotamarthi, R., Hayhoe, K., Mearns, L. O., Wuebbles, D., & Jacobs, J. (2021). Dynamical Downscaling. In Downscaling Techniques for High-Resolution Climate Projections (pp. 64-81). Cambridge University Press. DOI: 10.1017/9781108601269.005

PRECIS Model Usage for China’s Extreme Temperatures. (2024). Sustainability, 16(7), 3030. DOI: 10.3390/su16073030

Wilby, R. L., et al. (2004). Statistical downscaling of general circulation model output: A case study. Climate Research, 27, 211-229. DOI: 10.3354/cr027211

Hempel, S., Frieler, K., Warszawski, L., Schewe, J., & Piontek, F. (2013). A trend-preserving bias correction – the ISI-MIP approach. Earth System Dynamics, 4(2), 219-236. DOI: 10.5194/esd-4-219-2013

Gutmann, E., Barstad, I., Clark, M., Arnold, J., & Rasmussen, R. (2016). The intermediate complexity atmospheric research model (ICAR). Journal of Hydrometeorology, 17(3), 957-973.

Kochkov, D., Yuval, J., Langmore, I., Norgaard, P., Smith, J., Mooers, G., Klöwer, M., Lottes, J., Rasp, S., Düben, P. and Hatfield, S., 2024. Neural general circulation models for weather and climate. Nature, pp.1-7.

Moore, N., & Luo, L. (2021). Dynamical and statistical downscaling for hydrological predictions. Hydrology and Earth System Sciences, 25, 1205-1225. DOI: 10.5194/hess-25-1205-2021

Kuswanto, H., et al. (2021). Bias correction methods for climate impact projections. Journal of Climate, 34(5), 1751-1767. DOI: 10.1175/JCLI-D-20-0506.1

McSweeney, C. F., & Jones, R. G. (2016). The effect of bias correction on future climate projections. Climatic Change, 134, 635-646. DOI: 10.1007/s10584-015-1565-3

Pielke, R. A., et al. (2012). Dynamical downscaling: Assessment of value retained and added using the Regional Atmospheric Modeling System (RAMS). Journal of Geophysical Research: Atmospheres, 117, D05127. DOI: 10.1029/2011JD016630

Giorgi, F., & Mearns, L. O. (1999). Introduction to special section: Regional climate modeling revisited. Journal of Geophysical Research: Atmospheres, 104(D6), 6335-6352. DOI: 10.1029/98JD02072

Jang, S., & Kavvas, M. L. (2015). Downscaling global climate simulations to regional scales: statistical downscaling versus dynamical downscaling. Journal of Hydrologic Engineering, 20(1), A4014006.`

Christensen, J. H., & Christensen, O. B. (2003). Severe summertime flooding in Europe. Nature, 421(6925), 805-806. DOI: 10.1038/421805a

Leung, L. R., & Qian, Y. (2003). The sensitivity of precipitation and snowpack simulations to model resolution via dynamical downscaling of GCM output. Journal of Hydrometeorology, 4(6), 1025-1043. DOI: 10.1175/1525-7541(2003)004<1025, >2.0.CO;2

Le Roux, R., Katurji, M., Zawar-Reza, P., Quénol, H., & Sturman, A. (2018). Comparison of statistical and dynamical downscaling results from the WRF model. Environmental modelling & software, 100, 67-73.

Laprise, R. (2008). Regional climate modeling. Journal of Computational Physics, 227(7), 3641-3666. DOI: 10.1016/j.jcp.2006.10.024

Xu, Z., et al. (2020). Regional climate modeling for Australia: past performance and future projections. Climate Dynamics, 54, 3239-3263. DOI: 10.1007/s00382-020-05152-3

Feser, F., & Barcikowska, M. (2013). The influence of spectral nudging on typhoon formation and path in regional climate models. Climate Dynamics, 41, 1025-1045. DOI: 10.1007/s00382-013-1746-x

Di Luca, A., et al. (2013). Comparison of statistical and dynamical downscaling of precipitation over Australia from a global climate model. Journal of Geophysical Research: Atmospheres, 118(12), 585-604. DOI: 10.1002/jgrd.50139

Liu, C., et al. (2012). Dynamical downscaling of precipitation and temperature changes over China using a regional climate model with two parameterization schemes. Climate Dynamics, 39, 345-365. DOI: 10.1007/s00382-012-1412-5

Torma, C., et al. (2015). On the added value of regional climate modeling: Does a high-resolution model improve the simulation of precipitation? Monthly Weather Review, 143(2), 476-496. DOI: 10.1175/MWR-D-14-00034.1

Gao, X. J., et al. (2011). A comparison of downscaling techniques for producing high-resolution climate projections: application to the Yellow River basin, China. Climate Research, 47, 197-209. DOI: 10.3354/cr00981

Evans, J. P., & McCabe, M. F. (2013). Effect of model resolution on a regional climate model simulation over southeast Australia. Climate Research, 56, 131-145. DOI: 10.3354/cr01152

Teutschbein, C., & Seibert, J. (2012). Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. Journal of Hydrology, 456-457, 12-29. DOI: 10.1016/j.jhydrol.2012.05.052

Taylor, K. E., Stouffer, R. J., & Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bulletin of the American meteorological Society, 93(4), 485-498.

Andrews, T., Gregory, J. M., Webb, M. J., & Taylor, K. E. (2012). Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere‐ocean climate models. Geophysical research letters, 39(9).

Vandal, T., Kodra, E., & Ganguly, A. R. (2019). Intercomparison of machine learning methods for statistical downscaling: the case of daily and extreme precipitation. Theoretical and Applied Climatology, 137, 557-570.

Hobeichi, S., Nishant, N., Shao, Y., Abramowitz, G., Pitman, A., Sherwood, S., … & Green, S. (2023). Using machine learning to cut the cost of dynamical downscaling. Earth’s Future, 11(3), e2022EF003291.

Rhoades, A. M., Ullrich, P. A., & Zarzycki, C. M. (2018). Projecting 21st century snowpack trends in western USA mountains using variable-resolution CESM. Climate Dynamics, 50(1), 261-288.

Huang, X., Rhoades, A. M., Ullrich, P. A., & Zarzycki, C. M. (2016). An evaluation of the variable‐resolution CESM for modeling California’s climate. Journal of Advances in Modeling Earth Systems, 8(1), 345-369.

Zhang, T., Morcrette, C., Zhang, M., Lin, W., Xie, S., Liu, Y., … & Rodrigues, J. (2024). A Fortran-Python Interface for Integrating Machine Learning Parameterization into Earth System Models. Geoscientific Model Development Discussions, 2024, 1-26.

Teutschbein, C., & Seibert, J. (2012). Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. Journal of hydrology, 456, 12-29.

Mendez, M., Maathuis, B., Hein-Griggs, D., & Alvarado-Gamboa, L. F. (2020). Performance evaluation of bias correction methods for climate change monthly precipitation projections over Costa Rica. Water, 12(2), 482.

Vogel, E., Johnson, F., Marshall, L., Bende-Michl, U., Wilson, L., Peter, J. R., … & Duong, V. C. (2023). An evaluation framework for downscaling and bias correction in climate change impact studies. Journal of Hydrology, 622, 129693.

Hobeichi, S., Nishant, N., Shao, Y., Abramowitz, G., Pitman, A., Sherwood, S., … & Green, S. (2023). Using machine learning to cut the cost of dynamical downscaling. Earth’s Future, 11(3), e2022EF003291.

Jebeile, J., Lam, V., & Räz, T. (2021). Understanding climate change with statistical downscaling and machine learning. Synthese, 199, 1877-1897.

Pierce, D. W., & Cayan, D. R. (2016). Downscaling humidity with localized constructed analogs (LOCA) over the conterminous United States. Climate dynamics, 47, 411-431.

Gutmann, E. D., Hamman, J. J., Clark, M. P., Eidhammer, T., Wood, A. W., & Arnold, J. R. (2022). En-GARD: A statistical downscaling framework to produce and test large ensembles of climate projections. Journal of Hydrometeorology, 23(10), 1545-1561.

Seyyed Kaboli, H., AkhodAli, A. M., Masah Bavani, A. R., & Radmanesh, F. (2012). A Downscaling Model Based on K-nearest neighbor (K-NN) Non-parametric Method. Water and Soil, 26(4), 799-808.

Rhoades, Alan M., Colin M. Zarzycki, Héctor A. Inda‐Diaz, Mohammed Ombadi, Ulysse Pasquier, Abhishekh Srivastava, Benjamin J. Hatchett et al. “Recreating the California New Year’s flood event of 1997 in a regionally refined Earth system model.” Journal of Advances in Modeling Earth Systems 15, no. 10 (2023): e2023MS003793.

Kim, R.S., Kumar, S., Vuyovich, C., Houser, P., Lundquist, J., Mudryk, L., Durand, M., Barros, A., Kim, E.J., Forman, B.A. and Gutmann, E.D., 2020. Snow Ensemble Uncertainty Project (SEUP): quantification of snow water equivalent uncertainty across North America via ensemble land surface modeling. The Cryosphere Discussions, 2020, pp.1-32.

Akhter, S., Holloway, C.E., Hodges, K. and Vanniere, B., 2023. How well do high-resolution Global Climate Models (GCMs) simulate tropical cyclones in the Bay of Bengal?. Climate Dynamics, 61(7), pp.3581-3604.

Chen, J., Arsenault, R., Brissette, F.P. and Zhang, S., 2021. Climate change impact studies: Should we bias correct climate model outputs or post‐process impact model outputs?. Water Resources Research, 57(5), p.e2020WR028638.

Maraun, D. (2013). “Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue.” Journal of Climate, 26(6), 2137-2143.

Themeßl, M. J., Gobiet, A., & Leuprecht, A. (2011). “Empirical-statistical downscaling and error correction of daily precipitation from regional climate models.” International Journal of Climatology, 31(10), 1530-1544.